Partially order Plan dan Graph Plan

Dalam Bahasan ini kita akan membahas penyelesaian suatu contoh kasus  permasalahan Planning dengan menggunakan Partial order planning dan Graph Plan.

Permasalahan pertama:

Shopping (menggunakan algoritma Partial order Planning)

Langkah penyelesaian:

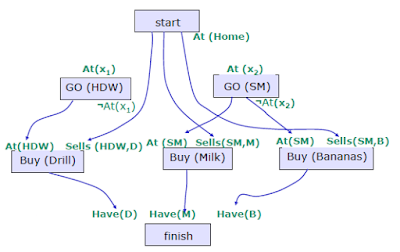
Tahap awal yaitu membuat langkah dari awal sampai ke finish seperti pada gambar diatas.

Tahap selanjutnya menambahkan go(HDW) sebagai (X1) untuk mencapai untuk mencapai at(HDW) dan menambahkan go(SM) sebagai (X₂) untuk mencapai at(SM).

Langkah selanjutnya kita bisa menjalankan langkah actian go(X₁) dan precond Go(HDW), dengan menggunakan effect at(Home). Serta menjalankan langkah action go(X₂) dan precond Go(SM), dengan menggunkan effect at(Home) seperti gambar diatas.

Setelah selesai dengan langkah sebelumnya, kita harus memperhatikan masalah apa saja yang mungkin terjadi yang bisa kita lihat pada gambar diatas. Pada gambar diatas, masalah terjadi dapat kita lihat pada bulatan yang ditunjuk oleh tanda panah, kita dapat memperhatikan bahwa Go(SM) tidak bisa tersambung ke at(Home) sebagai akibat sudah dimiliki oleh at(X₁), dan juga berlaku sebaliknya untuk Go(HDW).

\

Solusi yang dapat kita ambil, mungkin kita bisa memerlukan Go(SM) terjadi setelah Go(HDW). Kita bisa memutuskan untuk memenuhi at(X₂) dengan hasil at(HDW) Go(HDW) dan at(HDW) Go(HDW), tetapi jika kita menuju at(HDW) Go(HDW) kita tidak bisa menuju at(HDW) Sells(HDW,D).

Solusi yang dapat kita ambil dengan menempatkan Go(SM) antara GO(HDW) dan at(HDW) yang ditunjukan oleh tanda panah pada gambar diatas. Tetapi jika seperti itu kita harus menuju dua kali ke Go(HDW) karena sehabis ke Go(HDW) kita menuju Go(SM) dan balik lagi ke Go(HDW) untuk Buy(Drill).

Solusi yang dapat diambil dengan meletakan Go(SM) terjadi setelah Buy(Drill). Dengan menandakan nya dengan garis putus putus berwarna merah untuk memastikan bahwa hal ini terjadi.

Setelah kita berada di GO(SM) kita bisa Buy(Milk) dan Buy(Bananas) dan terakhir menuju at(Home).

Permasalahan kedua:

Birthday Dinner(menggunakan algoritma Graph Plan)

Langkah Penyelesaian:

Langkah awal dengan meletakkan di kondisi awal.

Masukan action yang dapat dilakukan dan hubungkan dengan Initial State.

Setelah itu, kita masukan hasil dari action yang dapat kita lakukan.

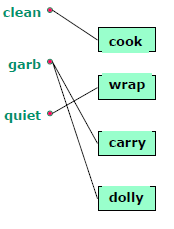
Selanjutnya, kita akan membuat mutex dari Graph Plan ini, alasannya bahwa tindakan dapat mutex adalah karena efek yang tidak konsisten. Dapat dilihat Clean mutex dengan Carry membuat Clean menjadi salah. Begitu juga dengan Garbage mutex dengan Carry dan Dolly membuat Garbage menjadi salah. Begitu juga dengan Quiet mutex dengan Dolly membuat quiet menjadi salah.

Alasan lain dari mutex adalah karena adanya gangguan: suatu action meniadakan precondition dari action lain. Dapat dilihat Carry mutex dengan Cook dan Dolly dan meniadakan precondition hasilnya, begitu juga dengan Wrap mutex dengan Dolly dan meniadakan precondition hasilnya

Pertama-tama, setiap proposisi mutex dengan bentuk yang negatif. Kemudian Karena alasan lain dari mutex adalah karena dukungan tidak konsisten. Jadi, Garbage mutex dengan not Clean dan not Quiet (karena untuk mendapatkan Garbage kita harus mempertahankan itu, yang mutex dengan Carry dan Dolly). Dinner mutex dengan not Clean (karena Cook dan Carry mutex pada level sebelumnya). Present mutex dengan not Quiet (karena Warp dan Dolly mutex pada level sebelumnya). Begitu juga dengan not Clean dan not Quiet (karena Carry dan Dolly mutex pada level sebelumnya).

Kita coba dengan cara lain, kita akan mendapatkan not Garbage dengan action Carry, dan Dinner dengan action Cook, tetapi Carrry dan Cook mutex jadi gagal.

Kita coba dengan cara lain, kita akan mendapatkan not Garbage dengan action Dolly, dan Dinner dengan action Cook, serta Present dengan action Wrap, tetapi Doly dan Wrap mutex.

Dikarenakan tidak ada cara lain untuk mendapatkan goal kita akan menggunakan depth two plan, yaitu menambahkan dua level lagi pada Graph.

Pada tahap ini kita mendapatkan mutex sama seperti di level sebelumnya

Pada level ini kita juga mendapatkan mutex yang sama dengan level sebelumnya, tetapi terdapat perbedaan yaitu pada level ini Dinner tidak mutex dengan Carry,karena kita bisa mendapatkan Dinner dengan membiarkannya dan tetap bisa melakukan Carry. Begitu juga dengan Present tidak mutex dengan Dolly karena kita bisa mendapatkan Present dengan membiarkannya dan dapat tetap melakukan Dolly.

Setelah kita selesai dengan mutex kita mencari lagi dengan cara seperti gambar diatas dan akhirnya dapat berhasil dengan cara seperti yang ditunjukan oleh gambar diatas.

Referensi :

http://whitenote03.blogspot.co.id/2016/10/penyelesaian-masalah-menggunakan.html

Sudoku solve with Algoritma Backtracking

CSP merupakan teknik yang dapat digunakan untuk penyelesaian persoalan dalam dunia nyata, yang terkadang memberikan batasan tertentu yang tidak boleh dilanggar pada saat mencari solusinya. Pada saat melakukan pencarian solusi atau pemilihan urutan aksi, teknik penyelesaian ini akan selalu menyesuaikan dengan constraint-constraint yang sudah ditentukan sebelumnya, sedemikian sehingga semua constraint akan terpenuhi. CSP dapat direpresentasikan sebagai berikut :

1. Kumpulan variabel. X --> kumpulan dari n variabel X1,X2,X3,…..,Xn, Variabel adalah elemen atau entity yang ingin dicari nilainya sehingga pemberian nilai pada variabel dapat menjadi solusi dari CSP.

2. Domain D --> Masing-masing variabel didefinisikan oleh suatu domain yang finite D1,D2,………,Dn, yang berisi kumpulan nilainilai yang mungkin untuk variabel tertentu yang bertujuan untuk menyelesaikan persoalan.

3. Constraint C --> kumpulan dari constraintconstraint C1,C2,……,Cm. Ci merupakan constraint-constraint yang berisi batasan nilai untuk setiap variabel dan tidak boleh dilanggar. Constraint-constraint ini akan membatasi domain dari suatu variabel sehingga menjadi lebih sempit

4. Assignment --> pemberian nilai pada suatu variabel.

5. Solusi --> pemberian nilai-nilai pada setiap variabel yang memenuhi semua constraint yang telah ditetapkan untuk persoalan, sehingga nilainilai variabel tersebut merupakan solusi untuk persoalan.

Untuk mempermudah pemahaman terhadap suatu CSP, maka umumnya persoalan ini digambarkan dalam bentuk graf, dan disebut constraint graph. Constraint graph terdiri dari simpul – simpul yang merepresentasikan variabel pada CSP yang akan dicari nilainya, dan busur pada graf menggambarkan constraint di antara variabel yang dihubungkannya. Jika dua variabel tidak terhubung dengan suatu busur, maka di antara dua variabel tersebut tidak memiliki hubungan constraint, jadi tidak perlu diperiksa kekonsistenannya pada saat pemberian nilai.

Tujuan utama dari penyelesaian CSP yaitu untuk memberikan nilai pada semua komponen persoalan, dengan tidak melanggar constraint yang telah ditetapkan untuk persoalan tersebut.

Deskripsi Umum Algoritma Backtracking Runut-balik (backtracking) adalah algoritma yang berbasis pada DFS untuk mencari solusi persoalan secara lebih mangkus. Runut-balik merupakan perbaikan dari algoritma exhaustive-search yang secara sistematis akan melakukan pencarian solusi permasalahan di antara semua kemungkinan solusi yang ada. Hanya pencarian yang mengarah ke solusi saja yang akan dipertimbangkan. Akibatnya, waktu pencarian dapat dihemat. Runut-balik lebih alami dinyatakan dalam algoritma rekursif. Untuk memfasilitasi pencarian ini, maka ruang solusi diorganisasikan ke dalam struktur pohon. Tiap simpul pohon menyatakan status (state) persoalan, sedangkan sisi (cabang) dilabeli dengan nilai – nilai x. Lintasan dari akar ke daun menyatakan solusi yang mungkin. Seluruh lintasan dari dari akar ke daun membentuk ruang solusi.

Stage Awal

Goal Stage

Deskripsi Umum Game Sudoku. Sudoku merupakan salah satu permainan yang sangat populer. Pada permainan ini akan terdapat kotak besar yang disusun oleh kotak-kotak kecil. Kota kecil akan tersusun oleh n2 space sebagai tempat untuk memposisikan angka. Kemudian kotak – kotak kecil terebut akan menyusun kotak besar sehingga ukuran kotak besar adalah n2 x n2 .

Objektif dari permainan ini adalah bagaimana kita bisa mengatur susunan angka – angka yang telah ditentukan kedalam suatu space pada kotak, dengan syarat bahwa angka pada kolom dan baris kotak besar tidak boleh sama demikian juga angka pada satu kotak kecil tidak boleh sama. Cara penyelesaian permainan ini dirancang dengan menggunakan algoritma backtracking dalam menemukan susunan angka yang sesuai untuk mengisi space – space yang ada sesuai dengan batasan yang telah dijelaskan sebelumnya, yaitu angka pada satu baris, satu kolom dan satu kotak kecil tidak boleh sama.

Dalam implementasinya , proses pencarian pada algoritma backtracking sebenarnya identik dengan penggunaan algoritma exhaustive-search namun dengan proses yang lebih sistematis. Secara garis besar langkah – langkah yang dilakukan oleh program dalam pencarian solusi adalah sebagai berikut :

1. Menguji sembarang nilai (0 < nilai < n+1) dengan fungsi pembatas yang ada.

2. a. Jika nilai tersebut memenuhi fungsi pembatas maka kotak akan terisi dengan nilai uji tersebut kemudian proses akan berpindah ke kotak berikutnya.

b. Jika nilai tersebut tidak memenuhi fungsi pembatas, maka program akan mengambil nilai  yang belum dipakai.

3. Jika semua opsi nilai pada domain nilai telah dicoba dan tidak ada satupun yang memenuhi fungsi pembatas, maka terjadi backtracking ke kotak sebelumnya. MAKALAH IF2251 STRATEGI ALGORITMIK TAHUN 2007

4. Pada kotak hasil backtracking ini, program akan menguji fungsi pembatas dengan nilai baru.

5. a. Jika nilai baru tersebut dapat memenuhi fungsi pembatas, maka nilai tersebut akan diisikan ke dalam kotak. Kemudian proses pengisian akan berpindah ke kotak berikutnya. b. Jika semua opsi nilai baru yang ada pada domain tidak dapat memenuhi fungsi pembatas maka akan terjadi lagi backtracking ke kotak sebelumnya.

 6. Program akan melakukan proses di atas secara rekursif sampai ditemukan penyelesaian atau tidak terdapat penyelesaian.

a. Terdapat penyelesaian : program berhasil mengisi semua kotak kosong yang tersedia dengan nilai yang memenuhi fungsi pembatas.

b. Tidak terdapat penyelesaian : setelah beberapa saat mencari solusi, ternyata program melakukan backtracking hingga kembali ke kotak pertama dan saat nilai indeks baris = -1 menandakan bahwa program tidak berhasil menemukan solusi.

Implementsi domain solusi permasalahan Himpunan ruang solusi terdiri :

{nilai| 0 < nilai < n+1; nilai є integer} dengan n adalah ukuran kotak kecil.

Implementsi fungsi –fungsi pembatas Sebagaimana telah saya sampaikan di atas game sudoku mempunyai fungsi pembatas yang cukup menarik dan unik, yaitu :

a. angka pada satu baris tidak boleh sama,

b. angka pada satu kolom tidak boleh sama, dan

c. angka pada satu kotak kecil tidak boleh sama.

               

        Berikut saya tampilkan source code dari ketiga fungsi pembatas tersebut, sengaja dituliskan dalam bahasa java untuk memudahkan pembaca bila ingin mencoba menjalankan ketiga fungsi tersebut tanpa perlu menerjemahkannya terlebih dahulu ke suatu bahasa pemrograman. Semoga dapat membantu dalam memahami fungsi batasan yang dimiliki permainan ini.

a.       

      A. Cek Kolom. Spesifikasi : Pada suatu kolom tidak boleh ditemukan 2 (dua ) nilai yang sama.

 B. Cek Baris. Spesifikasi : Pada suatu baris tidak boleh ditemukan 2 (dua) nilai yang sama.

  C.Cek Kotak Kecil. Spesifikasi : Pada suatu kotak kecil tidak boleh ditemukan 2 (dua) nilai yang             sama.

       Implementasi backtracking Sebagaimana pada sub bagian implementasi fungsi batasan, berikut saya sertakan source code dari algoritma backtracking yang telah dituliskan dalam bahasa java , semoga memudahkan pembaca dalam memahami algoritma tersebut.

  Kesimpulan Algoritma backtracking merupakan algoritma yang cukup mangkus untuk menyelesaikan berbagai persoalan. Hal ini disebabkan karena pada prinsipnya, kita tidak perlu memeriksa semua kemungkinan solusi yang ada. Pencarian hanya mengarah pada solusi yang dipertimbangkan saja. Oleh karena algoritma ini cukup efektif, maka backtracking banyak diterapkan dalam berbagai program game dan persoalan yang berkaitan dengan bidang kecerdasan buatan (artificial inteligence). Hasil analisis kemampuan algoritma backtracking dalam menyelesaikan persoalan pengisian sudoku menunjukkan bahwa algoritma ini cukup efektif untuk mendapatkan solusi persoalan tersebut. Sistem kerja algoritma backtracking yang sistematis dan ciri khasnya yang hanya memeriksa kemung-kinan solusi yang memang dapat dipertimbangkan untuk menjadi solusi akhir, diperkirakan dapat menjadi solusi yang efektif dan efisien untuk persoalan ini. 

sumber referensi : 

http://informatika.stei.itb.ac.id/~rinaldi.munir/Stmik/2005-2006/Makalah2006/MakalahStmik2006-47.pdf

http://informatika.stei.itb.ac.id/~rinaldi.munir/Stmik/2006-2007/Makalah_2007/MakalahSTMIK2007-096.pdf